학습 자료: 파이썬 머신러닝 완벽 가이드(개정2판), 위키북스
회귀
개요
통계학에서는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭
선형회귀 Y = W1*X1 + W2*X2 + W3*X3 + ... + Wn*Xn를 예로 들면 Y는 종속변수, X1, X2 ... Xn은 독립변수, W1, W2 ... Wn은 이 독립변수의 값에 영향을 미치는 회귀 계수(Regression coefficients)이다.
머신러닝 관점에서 본다면 독립변수는 피처에 해당되며 종속변수는 결정 값이다.
머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.
지도학습에서 분류와 회귀의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고 회귀는 연속형 숫자 값이라는 것이다.
종류
| 독립변수 개수 | 회귀 계수의 결합 |
| 1개: 단일 회귀 | 선형: 선형 회귀 |
| 여러 개: 다중 회귀 | 비선형: 비선형 회귀 |
여러 회귀 중 선형 회귀가 가장 많이 사용된다.
선형 회귀
개요
실제 값과 예측값의 차이(오류의 제곱 값)를 최소화하는 직선형 회귀선을 최적화하는 방식
규제(Regularization) 방법에 따라 다시 별도의 유형으로 나뉠 수 있다.
규제란?
일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 페널티 값을 적용하는 것
종류
1) 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제를 적용하지 않은 모델
2) 릿지(Ridge): 선형 회귀에서 L2 규제를 추가한 회귀 모델. L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델
3) 라쏘(Lasso): 선형 회귀에서 L1 규제를 추가한 회귀 모델. L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것. 피처 선택 기능으로도 불림.
4) 엘라스틱넷(ElasticNet): L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터셋에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정함.
5) 로지스틱 회귀(Logistic Regression): 분류에 사용되는 선형 모델. 이진 분류뿐 아니라 희소 영역의 분류(텍스트 분류 등)에서 뛰어난 예측 성능을 보임.
단순 선형 회귀를 통한 회귀 이해
단순 선형 회귀는 독립변수도 하나, 종속변수도 하나인 선형 회귀이다.
이는 기울기와 절편을 가진 1차 함수식으로 모델링할 수 있다.
즉, 예측값 Y=w0 + w1*X이다. 단순 선형 회귀에서는 이 기울기 w1과 절편 w0을 회귀 계수로 지칭한다.
그리고 회귀 모델을 이러한 1차 함수로 모델링했다면 실제 값은 이러한 1차 함수 값에서 실제 값만큼의 오류 값을 뺀(혹은 더한) 값이 된다.(w0 + w1*X + 오류 값)

이렇게 실제 값과 회귀 모델의 차이에 따른 오류 값을 잔차라고 부른다.
최적의 회귀 모델을 만든다는 것은 바로 전체 데이터의 잔차 합이 최소가 되는 모델을 만든다는 의미이고, 동시에 잔차 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다는 의미도 된다.
오류 값은 +나 -가 될 수 있기에 보통 오류 합을 계산할 때는 절댓값을 취해서 더하거나(Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식(RSS, Residual Sum of Square)을 취한다. RSS 방식으로 오류 합을 구하면 Error^2 = RSS이다.
이 RSS를 최소로 하는 w0, w1, 즉 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심 사항이다.

회귀에서 이 RSS는 비용(Cost)이며 w변수(회귀 계수)로 구성되는 RSS를 비용 함수 혹은 손실 함수(loss function)라고 한다.
머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값(즉, 오류 값)을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것이다.
경사하강법(Gradient Descent)
그렇다면 어떻게 비용 함수가 최소가 되는 W 파라미터를 구할 수 있을까?
경사하강법은 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식이다.
경사하강법은 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식이다.
경사하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나간다. 그리고 오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그때의 W 값을 최적 파라미터로 반환한다.
경사하강법의 핵심은 '어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?'이다. 비용 함수가 다음 그림과 같은 포물선 형태의 2차 함수라면 경사하강법은 최초 w에서부터 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 w를 업데이트한다. 마침내 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 w를 반환한다.
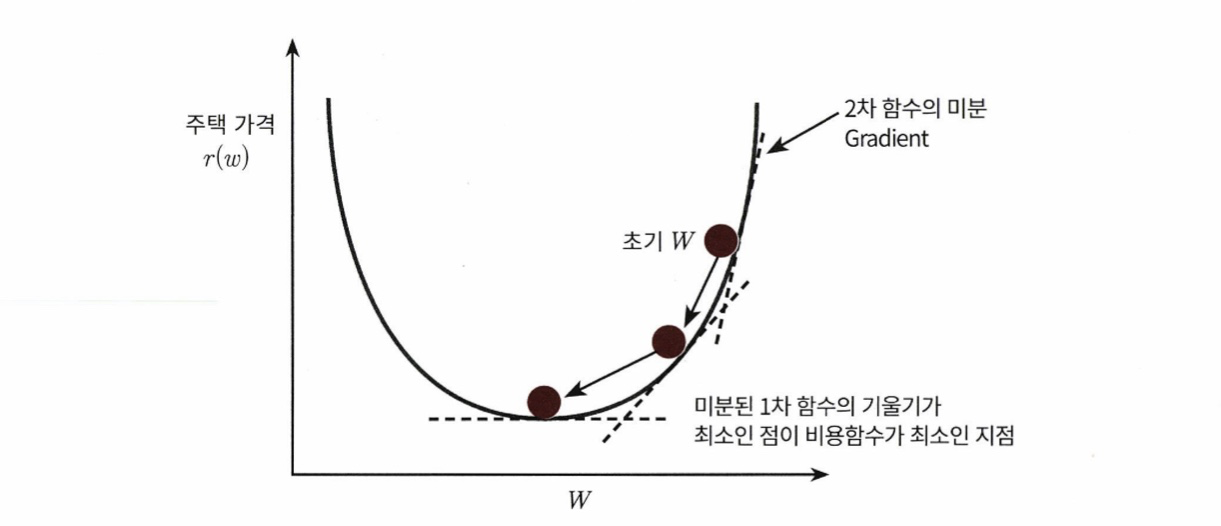
실제 계산에서는 w1, w0의 편미분 결괏값을 반복적으로 보정하면서 w1, w0 값을 업데이트하면 비용 함수가 최소가 되는 w1,w0의 값을 구할 수 있다. 업데이트는 새로운 w1을 이전 w1에서 편미분 결괏값을 마이너스(-)하면서 적용한다. 편미분 값이 너무 클 수 있기 때문에 여기에 보정 계수, 학습률을 곱한다.
경사하강법의 일반적인 프로세스는 다음과 같다.
Step 1: w1, w0를 임의의 값으로 설정하고 첫 비용 함수의 값을 계산한다.
Step 2: w1을 w1 - 학습률*w1편미분 값, w0을 w0 - 학습률*w0편미분 값으로 업데이트한 후 다시 비용 함수의 값을 계산한다.
Step 3: 비용 함수가 감소하는 방향성으로 주어진 횟수만큼 Step 2를 반복하면서 w1과 w0를 계속 업데이트한다.
일반적으로 경사하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기 때문에 수행 시간이 매우 오래 걸린다는 단점이 있다. 그 때문에 실전에서는 대부분 확률적 경사 하강법(Stochastic Gradient Descent)을 이용한다.
확률적 경사 하강법은 일부 데이터만 이용해 w가 업데이트되는 값을 계산하므로 경사하강법에 비해 빠른 속도를 보장한다.
지금까지 피처가 1개, 즉 독립변수가 1개인 단순 선형 회귀에서 경사하강법을 적용해 봤지만, 피처가 여러 개인 경우도 1개인 경우를 확장해 유사하게 도출할 수 있다.
피처가 한 개인 경우의 예측값 Y = w0 + w1*X로 회귀 계수를 도출한다. 피처가 M개(X1, X2, ..., X100) 있다면 그에 따른 회귀 계수도 M + 1(1개는 w0)개로 도출된다.
즉, Y = w0 + w1*X1 + w2*X2 + ... + w100*X100과 같이 예측 회귀식을 만들 수 있다.
사이킷런
LinearRegression()
예측값과 실제 값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스. OLS 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받는다. 피처 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해진다. 이러한 현상을 다중공선성(multi-collinearity) 문제라고 한다.
일반적으로 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용한다. 또한 매우 많은 피처가 다중 공선성 문제를 가지고 있다면 PCA를 통해 차원 축소를 수행하는 것도 고려해볼 수 있다.
회귀 평가 지표
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이 값을 기반으로 한 지표가 중심이다.
| 평가 지표 | 설명 |
| MAE | Mean Absolute Error. 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것. |
| MSE | Mean Squared Error. 실제 값과 예측값의 차이를 제곱해 평균한 것. |
| RMSE | Root Mean Squared Error. MSE가 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트를 씌운 것. |
| R^2 | 분산 기반으로 예측 성능을 평가. 1에 가까울수록 예측 정확도가 높다. 예측값 분산 / 실제값 분산 |
'ML' 카테고리의 다른 글
| [머신러닝/사이킷런] 회귀: 다항 회귀, 편향-분산 트레이드오프, 규제 선형 모델 (0) | 2025.03.03 |
|---|---|
| [머신러닝/사이킷런] 데이터 가공: 언더&오버 샘플링, 로그 변환, 이상치 제거 (0) | 2025.02.24 |
| [머신러닝/사이킷런] 하이퍼 파라미터 튜닝: 베이지안 최적화 (0) | 2025.02.23 |
학습 자료: 파이썬 머신러닝 완벽 가이드(개정2판), 위키북스
회귀
개요
통계학에서는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭
선형회귀 Y = W1*X1 + W2*X2 + W3*X3 + ... + Wn*Xn를 예로 들면 Y는 종속변수, X1, X2 ... Xn은 독립변수, W1, W2 ... Wn은 이 독립변수의 값에 영향을 미치는 회귀 계수(Regression coefficients)이다.
머신러닝 관점에서 본다면 독립변수는 피처에 해당되며 종속변수는 결정 값이다.
머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.
지도학습에서 분류와 회귀의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고 회귀는 연속형 숫자 값이라는 것이다.
종류
| 독립변수 개수 | 회귀 계수의 결합 |
| 1개: 단일 회귀 | 선형: 선형 회귀 |
| 여러 개: 다중 회귀 | 비선형: 비선형 회귀 |
여러 회귀 중 선형 회귀가 가장 많이 사용된다.
선형 회귀
개요
실제 값과 예측값의 차이(오류의 제곱 값)를 최소화하는 직선형 회귀선을 최적화하는 방식
규제(Regularization) 방법에 따라 다시 별도의 유형으로 나뉠 수 있다.
규제란?
일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 페널티 값을 적용하는 것
종류
1) 일반 선형 회귀: 예측값과 실제 값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제를 적용하지 않은 모델
2) 릿지(Ridge): 선형 회귀에서 L2 규제를 추가한 회귀 모델. L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델
3) 라쏘(Lasso): 선형 회귀에서 L1 규제를 추가한 회귀 모델. L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것. 피처 선택 기능으로도 불림.
4) 엘라스틱넷(ElasticNet): L2, L1 규제를 함께 결합한 모델. 주로 피처가 많은 데이터셋에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정함.
5) 로지스틱 회귀(Logistic Regression): 분류에 사용되는 선형 모델. 이진 분류뿐 아니라 희소 영역의 분류(텍스트 분류 등)에서 뛰어난 예측 성능을 보임.
단순 선형 회귀를 통한 회귀 이해
단순 선형 회귀는 독립변수도 하나, 종속변수도 하나인 선형 회귀이다.
이는 기울기와 절편을 가진 1차 함수식으로 모델링할 수 있다.
즉, 예측값 Y=w0 + w1*X이다. 단순 선형 회귀에서는 이 기울기 w1과 절편 w0을 회귀 계수로 지칭한다.
그리고 회귀 모델을 이러한 1차 함수로 모델링했다면 실제 값은 이러한 1차 함수 값에서 실제 값만큼의 오류 값을 뺀(혹은 더한) 값이 된다.(w0 + w1*X + 오류 값)

이렇게 실제 값과 회귀 모델의 차이에 따른 오류 값을 잔차라고 부른다.
최적의 회귀 모델을 만든다는 것은 바로 전체 데이터의 잔차 합이 최소가 되는 모델을 만든다는 의미이고, 동시에 잔차 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다는 의미도 된다.
오류 값은 +나 -가 될 수 있기에 보통 오류 합을 계산할 때는 절댓값을 취해서 더하거나(Mean Absolute Error), 오류 값의 제곱을 구해서 더하는 방식(RSS, Residual Sum of Square)을 취한다. RSS 방식으로 오류 합을 구하면 Error^2 = RSS이다.
이 RSS를 최소로 하는 w0, w1, 즉 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심 사항이다.

회귀에서 이 RSS는 비용(Cost)이며 w변수(회귀 계수)로 구성되는 RSS를 비용 함수 혹은 손실 함수(loss function)라고 한다.
머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값(즉, 오류 값)을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류 값을 구하는 것이다.
경사하강법(Gradient Descent)
그렇다면 어떻게 비용 함수가 최소가 되는 W 파라미터를 구할 수 있을까?
경사하강법은 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식이다.
경사하강법은 점진적으로 반복적인 계산을 통해 W 파라미터 값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터를 구하는 방식이다.
경사하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지는 방향성을 가지고 W 파라미터를 지속해서 보정해 나간다. 그리고 오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소 비용으로 판단하고 그때의 W 값을 최적 파라미터로 반환한다.
경사하강법의 핵심은 '어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?'이다. 비용 함수가 다음 그림과 같은 포물선 형태의 2차 함수라면 경사하강법은 최초 w에서부터 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 w를 업데이트한다. 마침내 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 그때의 w를 반환한다.

실제 계산에서는 w1, w0의 편미분 결괏값을 반복적으로 보정하면서 w1, w0 값을 업데이트하면 비용 함수가 최소가 되는 w1,w0의 값을 구할 수 있다. 업데이트는 새로운 w1을 이전 w1에서 편미분 결괏값을 마이너스(-)하면서 적용한다. 편미분 값이 너무 클 수 있기 때문에 여기에 보정 계수, 학습률을 곱한다.
경사하강법의 일반적인 프로세스는 다음과 같다.
Step 1: w1, w0를 임의의 값으로 설정하고 첫 비용 함수의 값을 계산한다.
Step 2: w1을 w1 - 학습률*w1편미분 값, w0을 w0 - 학습률*w0편미분 값으로 업데이트한 후 다시 비용 함수의 값을 계산한다.
Step 3: 비용 함수가 감소하는 방향성으로 주어진 횟수만큼 Step 2를 반복하면서 w1과 w0를 계속 업데이트한다.
일반적으로 경사하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기 때문에 수행 시간이 매우 오래 걸린다는 단점이 있다. 그 때문에 실전에서는 대부분 확률적 경사 하강법(Stochastic Gradient Descent)을 이용한다.
확률적 경사 하강법은 일부 데이터만 이용해 w가 업데이트되는 값을 계산하므로 경사하강법에 비해 빠른 속도를 보장한다.
지금까지 피처가 1개, 즉 독립변수가 1개인 단순 선형 회귀에서 경사하강법을 적용해 봤지만, 피처가 여러 개인 경우도 1개인 경우를 확장해 유사하게 도출할 수 있다.
피처가 한 개인 경우의 예측값 Y = w0 + w1*X로 회귀 계수를 도출한다. 피처가 M개(X1, X2, ..., X100) 있다면 그에 따른 회귀 계수도 M + 1(1개는 w0)개로 도출된다.
즉, Y = w0 + w1*X1 + w2*X2 + ... + w100*X100과 같이 예측 회귀식을 만들 수 있다.
사이킷런
LinearRegression()
예측값과 실제 값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스. OLS 기반의 회귀 계수 계산은 입력 피처의 독립성에 많은 영향을 받는다. 피처 간의 상관관계가 매우 높은 경우 분산이 매우 커져서 오류에 매우 민감해진다. 이러한 현상을 다중공선성(multi-collinearity) 문제라고 한다.
일반적으로 상관관계가 높은 피처가 많은 경우 독립적인 중요한 피처만 남기고 제거하거나 규제를 적용한다. 또한 매우 많은 피처가 다중 공선성 문제를 가지고 있다면 PCA를 통해 차원 축소를 수행하는 것도 고려해볼 수 있다.
회귀 평가 지표
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이 값을 기반으로 한 지표가 중심이다.
| 평가 지표 | 설명 |
| MAE | Mean Absolute Error. 실제 값과 예측값의 차이를 절댓값으로 변환해 평균한 것. |
| MSE | Mean Squared Error. 실제 값과 예측값의 차이를 제곱해 평균한 것. |
| RMSE | Root Mean Squared Error. MSE가 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트를 씌운 것. |
| R^2 | 분산 기반으로 예측 성능을 평가. 1에 가까울수록 예측 정확도가 높다. 예측값 분산 / 실제값 분산 |
'ML' 카테고리의 다른 글
| [머신러닝/사이킷런] 회귀: 다항 회귀, 편향-분산 트레이드오프, 규제 선형 모델 (0) | 2025.03.03 |
|---|---|
| [머신러닝/사이킷런] 데이터 가공: 언더&오버 샘플링, 로그 변환, 이상치 제거 (0) | 2025.02.24 |
| [머신러닝/사이킷런] 하이퍼 파라미터 튜닝: 베이지안 최적화 (0) | 2025.02.23 |
