학습 자료: 파이썬 머신러닝 완벽 가이드(개정2판), 위키북스
다항 회귀
개요
회귀가 독립변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현되는 것y = w0 + w1*x1 + w2*x2 + w3*x1*x2 + w4*x1^2 + w5*w2^2회귀에서 선형/비선형 회귀를 나누는 기준은 회귀 계수에 따른 것이기 때문에 다항 회귀도 선형 회귀이다.
사이킷런
PolynomialFeatures()단항식 피처를 다항식 피처로 변환- degree: 다항식의 차수
다항 회귀를 이용한 과소적합 및 과적합 이해
다항식의 차수가 높아질수록 매우 복잡한 피처 간의 관계까지 모델링이 가능하다.하지만 다항 회귀의 차수(degree)가 높아질수록 과적합의 문제가 크게 발생한다.
결론적으로, 학습 데이터의 패턴을 잘 반영하면서도 복잡하지 않은 균형 잡힌(Balanced) 모델이 되어야 한다.
편향-분산 트레이드오프(Bias-Variance Trade off)
Degree 1과 같은 모델은 매우 단순화된 모델로서 고편향(High Bias)성을 가졌다고 표현한다.반대로 Degree 15와 같은 모델은 매우 복잡한 모델로 고분산(High Variance)성을 가졌다고 표현한다.
일반적으로 편향과 분산을 한쪽이 높으면 한쪽이 낮아지는 경향이 있다.
즉, 편향이 높으면 분산은 낮아지고(과소적합) 반대로 분산이 높으면 편향이 낮아진다(과적합).
높은 편향/낮은 분산: 과소적합(Underfit)
낮은 편향/높은 분산: 과적합(Overfit)
규제 선형 모델: 릿지, 라쏘, 엘라스틱넷
개요
이전까지 선형 모델의 비용 함수는 RSS를 최소화하는, 즉 실제 값과 예측값의 차이를 최소화하는 것만 고려했다.
그러다 보니 학습 데이터에 지나치게 맞추게 되고, 회귀 계수가 쉽게 커지며 과적합이 발생했다.
이를 반영해 비용 함수는 1)학습 데이터의 잔차 오류 값을 최소로 하는 RSS 최소화 방법과 2) 과적합을 방지하기 위해 회귀 계수 값이 커지지 않도록 하는 방법이 서로 균형을 이뤄야 한다.
이렇게 회귀 계수의 크기를 제어해 과적합을 개선하려면 비용 함수의 목표가 다음과 같이 변경될 수 있다.
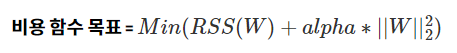
여기서 alpha는 학습 데이터 적합 정도와 회귀 계수 값의 크기 제어를 수행하는 튜닝 파라미터이다.
alpha를 0에서부터 지속적으로 값을 증가시키면 회귀 계수 값의 크기를 감소시킬 수 있다.
이처럼 비용 함수에 alpha 값으로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제(Regularization)라고 부른다.
릿지(Lidge) 회귀
W의 제곱에 대해 페널티를 부여하는 L2 규제를 적용한 회귀
회귀 계수의 크기를 감소시킴
Ridge()
- alpha: L2 규제 계수

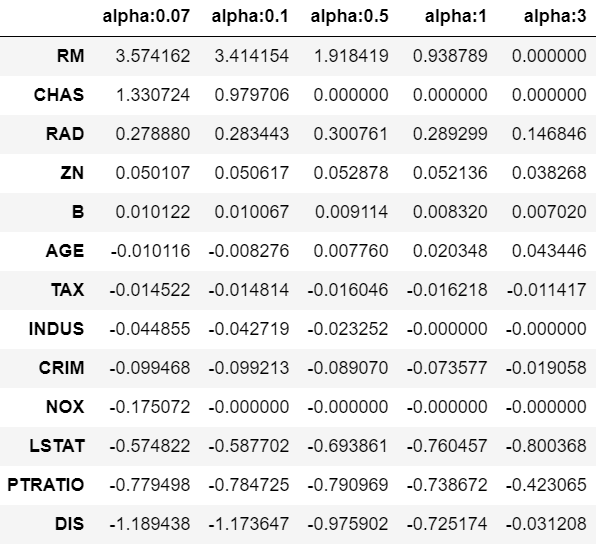
라쏘(Lasso) 회귀
W의 절댓값에 페널티를 부여하는 L1 규제를 적용한 회귀
불필요한 회귀 계수를 0으로 만들고 제거(피처 선택)
Lasso()
- alpha: L1 규제 계수

엘라스틱넷(Elastic Net) 회귀
L2 규제와 L1 규제를 결합한 회귀
라쏘 회귀가 회귀 계수를 0으로 만드면서 회귀 계수의 값이 급격히 변동하는 성향을 완화하기 위해 L2 규제를 추가한 개념
ElasticNet()
- alpha: a + b(a * L1 + b * L2)
- l1_ratio: a / (a + b)
'ML' 카테고리의 다른 글
| [머신러닝/사이킷런] 회귀: 데이터 변환(로그 변환), 로지스틱 회귀, 회귀 트리 (0) | 2025.03.04 |
|---|---|
| [머신러닝/사이킷런] 회귀: 선형 회귀, 경사하강법, 평가 (0) | 2025.02.26 |
| [머신러닝/사이킷런] 데이터 가공: 언더&오버 샘플링, 로그 변환, 이상치 제거 (0) | 2025.02.24 |
